Fun with Turtle Geometry

8 June 2018

Turtle Geometry [1] is an excellent book that shows how far one can get with a little coding. I wrote a small library in Racket that can run all 2d code examples from the book without much conversion. 

#lang racket
(require "../src/Racket/turtle/turtle-graphics.rkt")

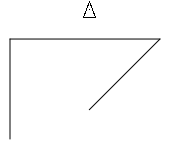
(clear 1000 1000)
(forward 100)
(turn 90)
(forward 150)
(turn -45)
(back 100)
(turn -45)
(penup)
(forward 100)
(show)

first-turtle0.png 

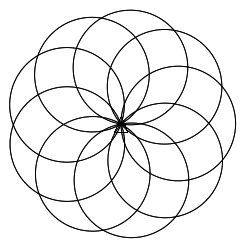
(clear 1000 1000)

(define (arcr r deg)
  (for ([i deg])
    (forward r)
    (turn 1)))

(define (circles n)
  (for ([i n])
    (arcr 1 360)
    (turn 40)))

(circles 9)

(show)

first-turtle1.png 

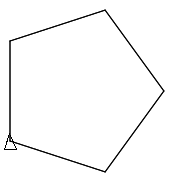
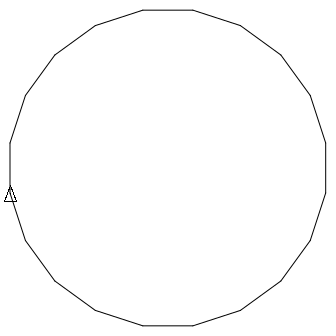
(clear 1000 1000)

(define (poly side angle steps)
  (for ([step steps])
    (forward side)
    (turn angle)))

(poly 100 72 10)

(show)

first-turtle2.png 

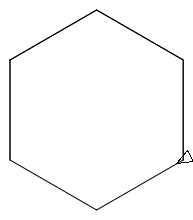
(clear 1000 1000)
(poly 100 60 10)
(show)

first-turtle21.png 

(clear 1000 1000)
(poly 50 18 20)
(show)

first-turtle22.png 

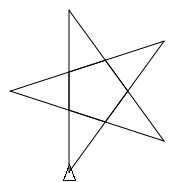
(clear 1000 1000)

(define (newpoly side angle steps)
  (for ([step steps])
    (forward side)
    (turn angle)
    (forward side)
    (turn (* 2 angle))))

(newpoly 100 72 5)
(show)

first-turtle3.png 

(clear 1000 1000)
(poly 100 121 20)
(show)

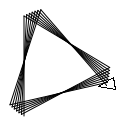
first-turtle4.png 

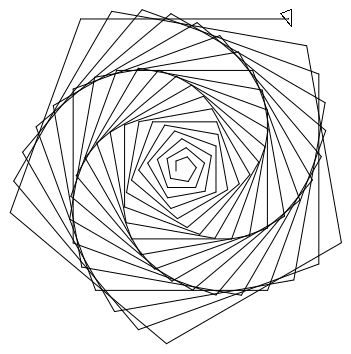
(clear 1000 1000)

(define (polyspi side angle steps)
  (when (>= steps 1)
    (forward side)
    (turn angle)
    (polyspi (+ side 2) angle (- steps 1))))

(polyspi 10 95 100)
(show)

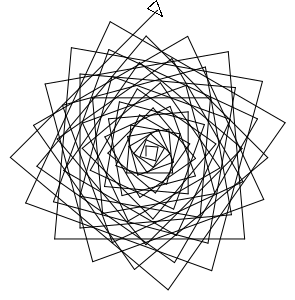
first-turtle5.png 

(clear 1000 1000)
(polyspi 10 70 100)
(show)

first-turtle6.png

References

[1] Harold Abelson and Andrea A. diSessa. Turtle Geometry: The Computer as a Medium for Exploring Mathematics. The MIT Press, Cambridge, Massachussets, London, England, 1980.

Peter Samarin